概述
Monte Carlo Method (MCM)蒙特卡洛方法,是一类随机算法的统称,这些算法的共性是使用重复的随机抽样来进行数值计算。MCM获得的是相应问题的数值近似结果,采样次数越多,越接近真实值,即MCM一定会产出一个结果,且结果是近似的。如Sobol所述:
The Monte Carlo method is a numerical method of solving mathematical problems by random sampling (or by the simulation of random variables).
与Monte Carlo Method相对应的是Las Vegas Method (LVM)。LVM同样采用随机算法,但是与MCM不同,LVM的目标是产出准确结果。但是LVM所作的随机性决策有可能导致算法找不到所需的解。最典型的LVM算法是Quick Sort,Quick Sort每次随机选择一个pivot,但是最终总能给出准确的排序结果。
对比MCM和LVM,举个例子,假如筐里有100个苹果,每次闭眼拿1个,挑出最大的。首先随机拿1个,再随机拿1个跟它比,留下大的,再随机拿1个……每拿一次,留下的苹果都至少不比上次的小。拿的次数越多,挑出的苹果就越大,但除非拿100次,否则无法肯定挑出了最大的。这个挑苹果的算法,就属于蒙特卡罗算法——尽量找好的,但不保证是最好的。而拉斯维加斯算法,则是另一种情况。假如有一把锁,给我100把钥匙,只有1把是对的。于是我每次随机拿1把钥匙去试,打不开就再换1把。我试的次数越多,打开(最优解)的机会就越大,但在打开之前,那些错的钥匙都是没有用的。这个试钥匙的算法,就是拉斯维加斯的——尽量找最好的,但不保证能找到。
既然LVM可以给出准确解,为何还需要MCM呢?很多情况下,问题无法无法使用准确的数学/数值计算方法求解,或者求解成本非常高,而MCM可以在有效的时间内给出近似的结果。
为了使用MC算法,我们首先去要进行随机抽样,后面我将详细介绍常见的抽样算法。这里我先介绍两个例子,展示MCM的核心思想。
示例1——计算圆周率
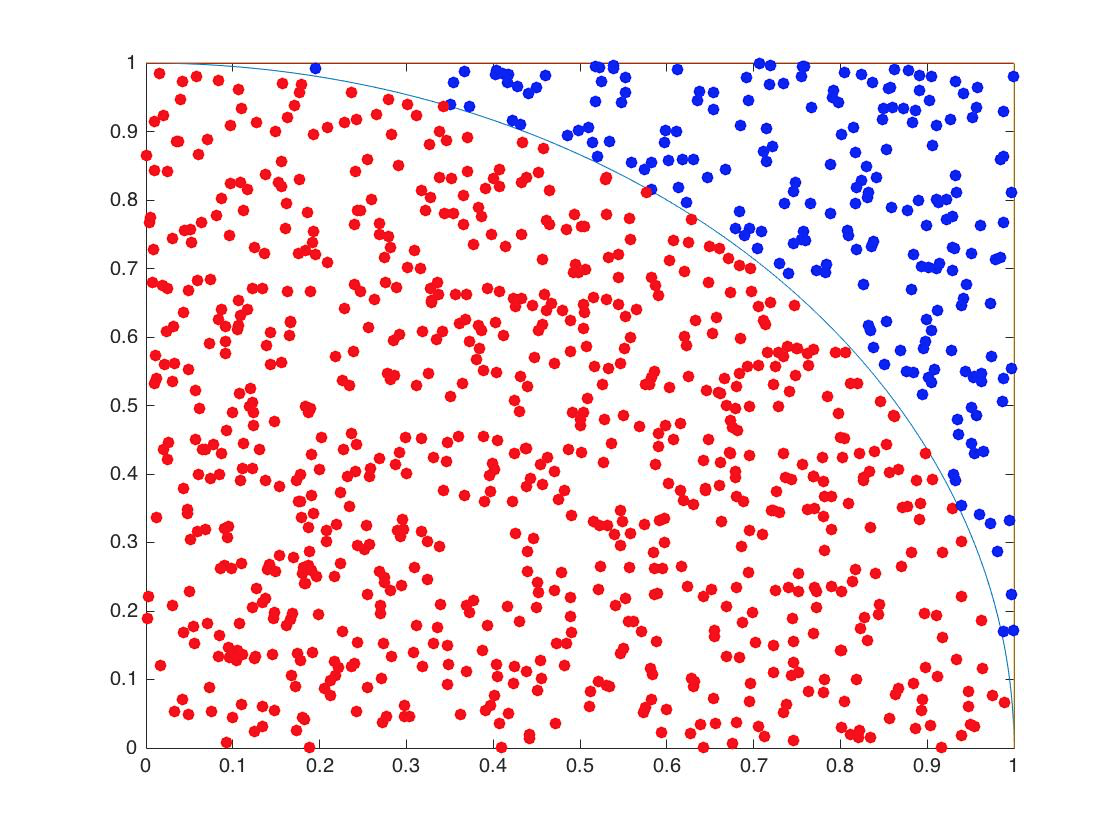
为了计算圆周率,我们可以在下图的正方形中随机生成大量的点,落在下图圆弧中的点(图中红色的点)的数量,和总的点的数量的比,我们可以认为是四分之一圆和正方形面积之比。
matlab示例代码如下:
totalCount=3000000;
hitCount=0;
for i=1:totalCount
point=rand(1,2);
dist=sqrt(point(1)^2+point(2)^2);
if dist<=1
hitCount=hitCount+1;
end
end
estimatedPi=hitCount/totalCount*4
示例2——计算定积分
设一组随机变量${X_i}$在$[a,b]$上独立同分布,分布律为$f_X$,即$f_X$是随机变量$X$的PDF。令$g^(x)=\frac{g(x)}{f_X(x)}$,则$g^(x)$也是一组独立同分布的随机变量。
根据Law of the unconscious statistician(abbr. LOTUS)可以得到: 根据强大数定理可以得到: 即以概率1收敛至$I$。也就是说,当样本$X$数量足够大,上述均值可以做为期望值。
假设我们所要求的积分为,我们任意选择一个方便进行抽样的PDF为$f_X(x)$,使$\int_a^bf_X(x)dx=1$,令,那么目标积分可以写成,结合上面根据LOTUS推断出的结论,可以得到求积分$I$的具体步骤是:
- 从PDF $f_X$中采样,获取样本集$X_i\ (i=1,2,\cdot\cdot\cdot,N)$
- 计算均值,做为$I$的近似值。
特别地,针对$f_X$,我们可以取$[a,b]$上的均匀分布,即,那么前面所述的,积分$\int_a^bg(x)dx$就可以通过计算来获得。
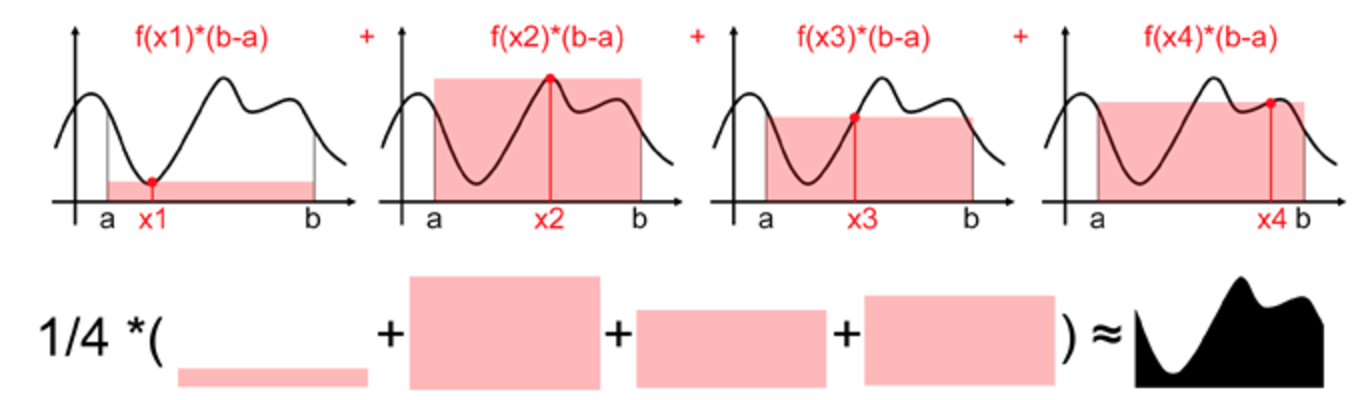
关于均值法计算定积分的直观解释,可以查看这篇文章。这里简单说一下。在$[a,b]$之间随机取一个点$x_i$,图中暗色部分的面积即为$f(x_i)*(b-a)$,多次取点后的面积平均值即为所求积分。