概述
- 示例
- Box-Muller变换

概述

Inverse transform sampling，称为逆变换采样。本质上来说，计算机只能基于均匀分布进行采样，怎么处理才能使计算机能对较为复杂的PDF进行采样呢？ITS就是最简单的一种方法。设$f(x)$为目标采样的分布（即PDF），$F(x)$为其累积分布函数（即CDF）。我们可以在$[0,1]$上进行基于均匀分布的采样${x_1,x_2,\cdot\cdot\cdot,x_i}$，然后反求$F^{-1}(x_i)$，所得的结果就是符合$f(x)$分布的采样结果。

示例

已知一个分布的PDF为 $h(x)=\frac{2m^2}{(1-m^2)x^3}, x\in[m,1]$ ，可以求得对应的CDF为： $H(x)=\int_{-\infty}^{x}h(t)dt=\left\{\begin{array}\\{0} & if\ x<m\\\frac{1}{1-m^2}-\frac{m^2}{(1-m^2)x^2} & if\ x\in[m,1]\\1 & if\ x>1\end{array}\right.$ CDF的反函数为： $H^{-1}(x)=\sqrt{\frac{m^2}{1-(1-m^2)x}},\ x\in{[0,1]}$

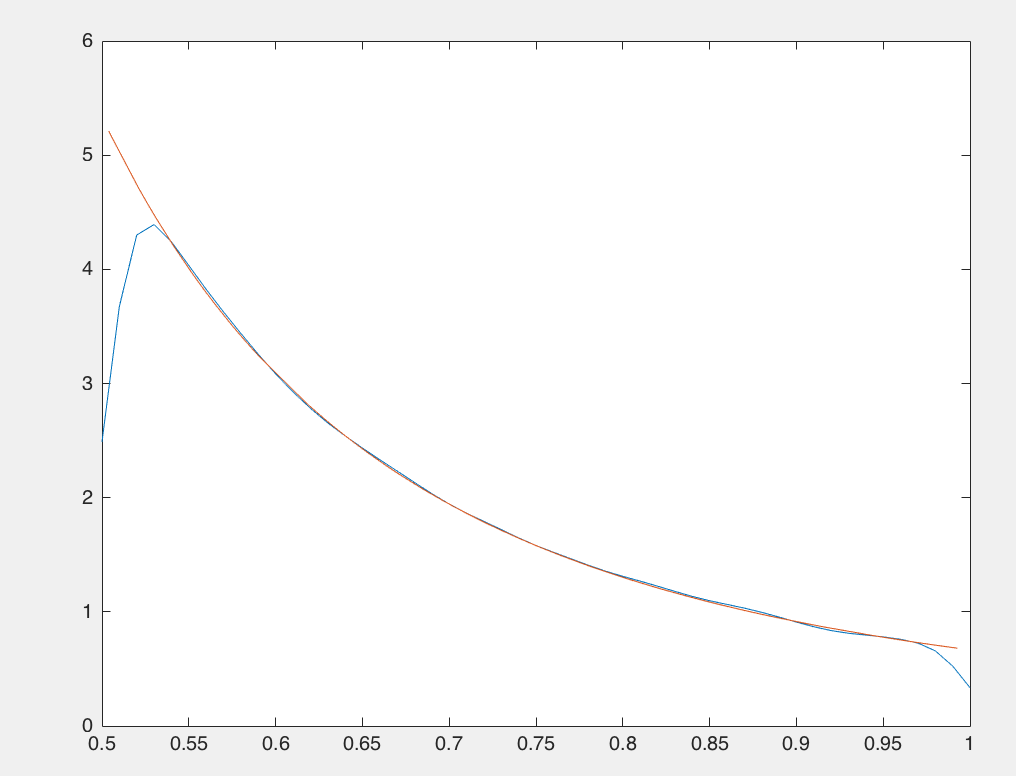
使用inverse transform sampling的matlab代码和对比图如下：

my_pdf

function [y] = my_pdf(x,m)
y=2*m^2/(1-m^2)./power(x,3);

my_inverse_cdf

function [y] = my_inverse_cdf(x,m)
y=sqrt(m^2./(1-(1-m^2)*x));

sampling

samplingY=sort(unifrnd(0,1,1,100000));
m=0.5;
samplingX=my_inverse_cdf(samplingY,m)
x=sort(unifrnd(m,1,1,100));
y=my_pdf(x,m);
ksdensity(samplingX,m:0.01:1);
hold on;
plot(x,y);

Alt text

Box-Muller变换

Box-Muller Transform 是一种利用均匀分布产生正态分布的方法，目前很多软件内置的正态分布采样方法都采用了Box-Muller transform。方法具体内容：如果$U_1$和$U_2$相互独立且服从正态分布，即$U_1,U_2\sim{Uniform[0,1]}$，则 $Z_0=\sqrt{-2lnU_1}\cos{(2πU_2)}$ $Z_1=\sqrt{-2lnU_1}\cos{(2πU_2)}$ 独立且服从标准正态分布。

以下为简单的推导过程：

假设$X\sim{N[0,1]}, Y\sim{N[0,1]}$，我们的目标是使用均匀分布产生X和Y；
联合分布 $p(x,y)=p(x)*p(y)=\frac{1}{2π}e^{-\frac{x^2+y^2}{2}}=\frac{1}{2π}e^{-\frac{r^2}{2}}$ ，其中$x=r\sin\theta,y=r\cos\theta$
上述分布看作$\theta$和$r$的联合分布，我们获得$\theta$和$r$的样本后，即可得到$x$和$y$的样本。
前半部分看作$\theta$的分布，$\theta\sim{Unif[0,2π]}\sim{2πU_1}$。如何获得符合该分布的$\theta$样本？— 均匀分布。
后半部分看作$r$的分布，$p(r)=e^{-r^2/2}$，如何获取符合该分布的$r$样本？— Inverse Transform Sampling。后半部分的CDF的反函数为 $F^{-1}(\mu)=\sqrt{-2log(1-\mu)}=\sqrt{-2log\mu'}$ ，均匀采样$\mu’$后根据反函数反求样本即可。
根据以上， $x=r\sin\theta=\sqrt{-2logU_2}*\sin{(2πU_1)}$ $y=r\cos\theta=\sqrt{-2logU_2}*\cos{(2πU_1)}$
如果要获得期望为$\mu$，方差为$\sigma^2$的正态分布，返回$x*\sigma+\mu$即可

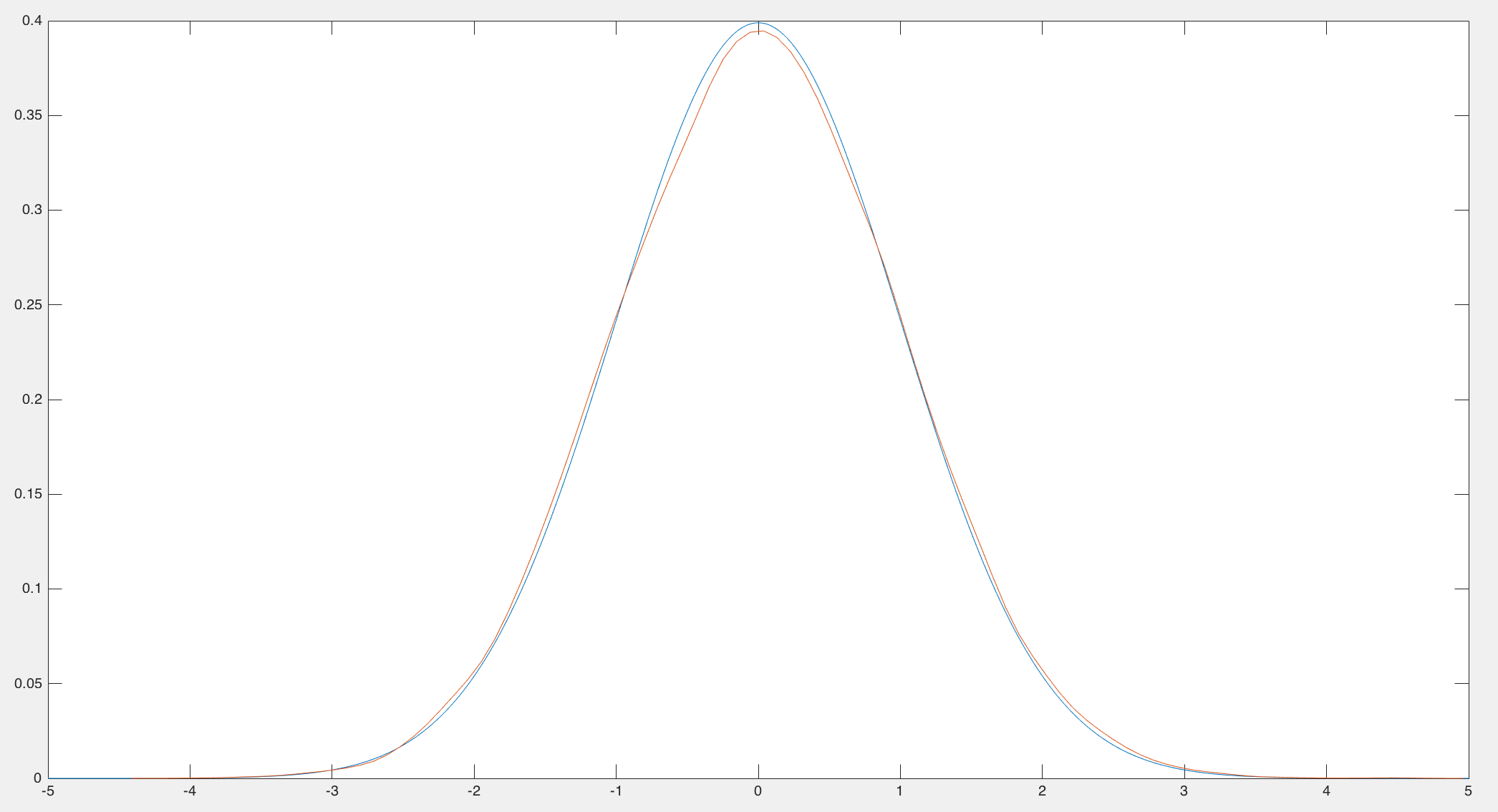
Matlab代码和采样效果图如下。

box_muller.m

function [z0,z1] = box_muller()
u1=unifrnd(0,1,1,1);
u2=unifrnd(0,1,1,1);
z0=sqrt(-2*log(u1))*sin(2*pi*u2);
z1=sqrt(-2*log(u1))*cos(2*pi*u2);

box_muller_sampling.m

c=[]
for i=1:10000
[a,b]=box_muller();
c=[c,a,b];
end
x = -5:0.01:5;
y = normpdf(x, 0, 1);
plot(x,y);
hold on;
[f,xc]=ksdensity(c);
plot(xc,f);

Alt text

Inverse Transforming Sampling

逆变换采样

概述

示例

Box-Muller变换

FEATURED TAGS

FRIENDS