Reject Sampling

• 概述
• 示例
• Adaptive Reject Sampling

概述

之前我们提到了基于CDF的inverse transform sampling，但是存在很多情况，我们无法或者很难从PDF求出CDF，即使求得了CDF，也很难求CDF的反函数。这个时候就很难直接使用ITS。拒绝采样（Reject Sampling）可以解决此问题。

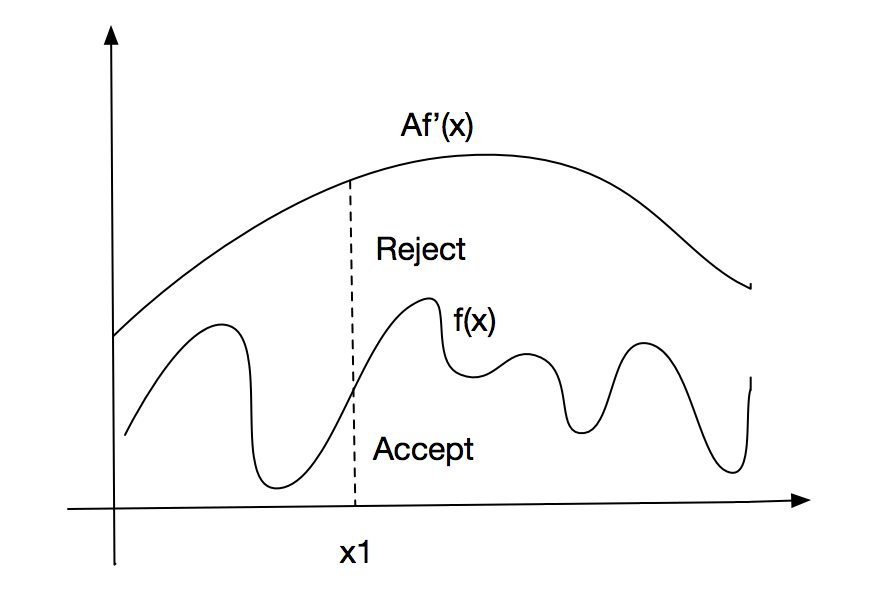
参考上图，拒绝采样步骤如下：

• 针对目标采样分布$f(x)$，选择$f'(x)$和常数$A$，使对任意$x$，有$f(x)<Af'(x)$；
• 针对$f'(x)$进行采样，获得样本$x_i$；
• 计算$p=\frac{f(x_i)}{Af'(x_i)}$；
• 从[0,1]中随机生成值$p'$；
• 如果$p>=p'$，则保留样本$x_i$，否则拒绝；

示例

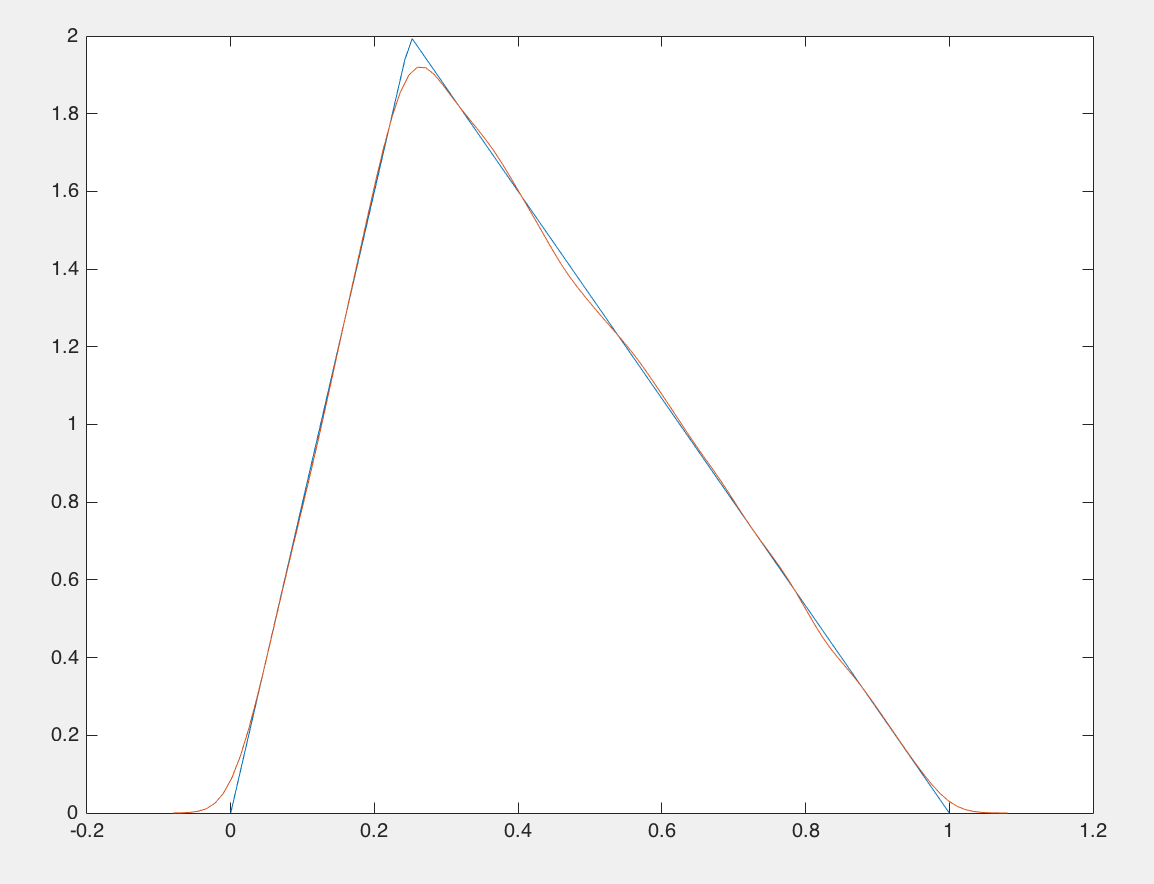
• f.m

  function y=f(x)
  if (0<=x) && (x<0.25)
    y=8*x;
  elseif (0.25<=x) && (x<1)
    y=8/3-8/3*x;
  else
    y=0;
  end
  

• f2.m

  function y=f2(x)
  y=1;
  

• reject_sampling.m

  c = [];
  for i=1:100000
  x_i = unifrnd(0,1,1,1);
  accept_prob = f(x_i)/(2*f2(x_i));
  p_ = unifrnd(0,1,1,1);
  if p_ < accept_prob
    c=[c,x_i];
  end
  end
  x = linspace(0,1);
  plot(x,arrayfun(@f,x));
  hold on;
  ksdensity(c);
  

Adaptive Reject Sampling

上述拒绝采样可以弥补IFS不适用的一些情况，但是有个缺点，即样本接受率太低，造成大量样本的浪费。

对于特殊的凹函数，我们可以如下处理：

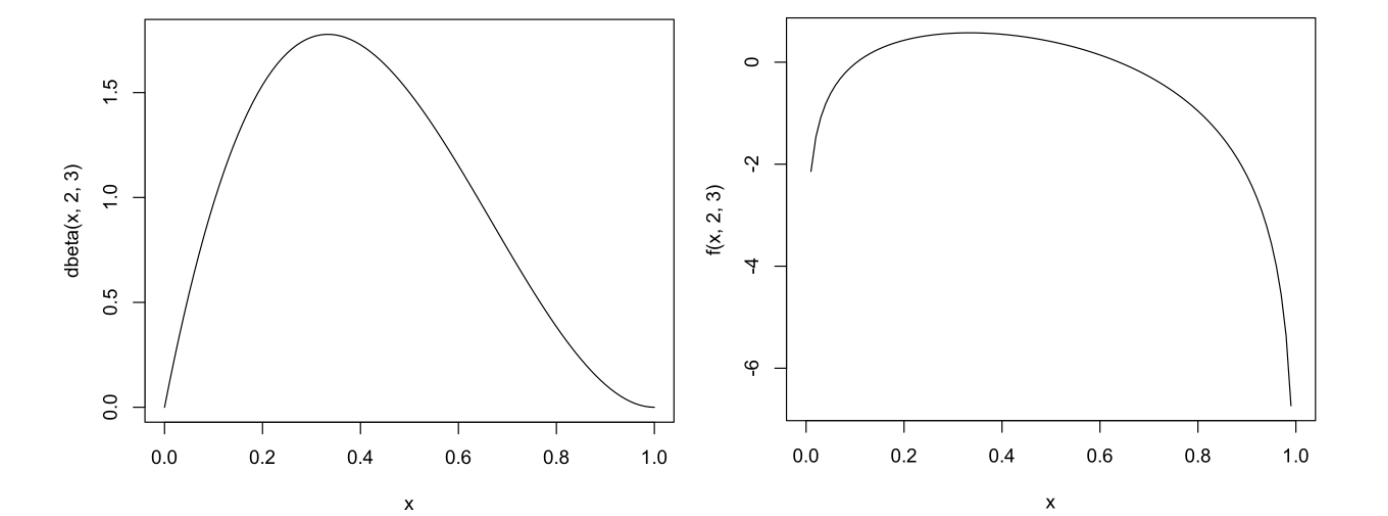
• 求对数，下左图为原始$f(x)$，下右图为对数图像；
• 针对对数图像取多个切平面，如下图；
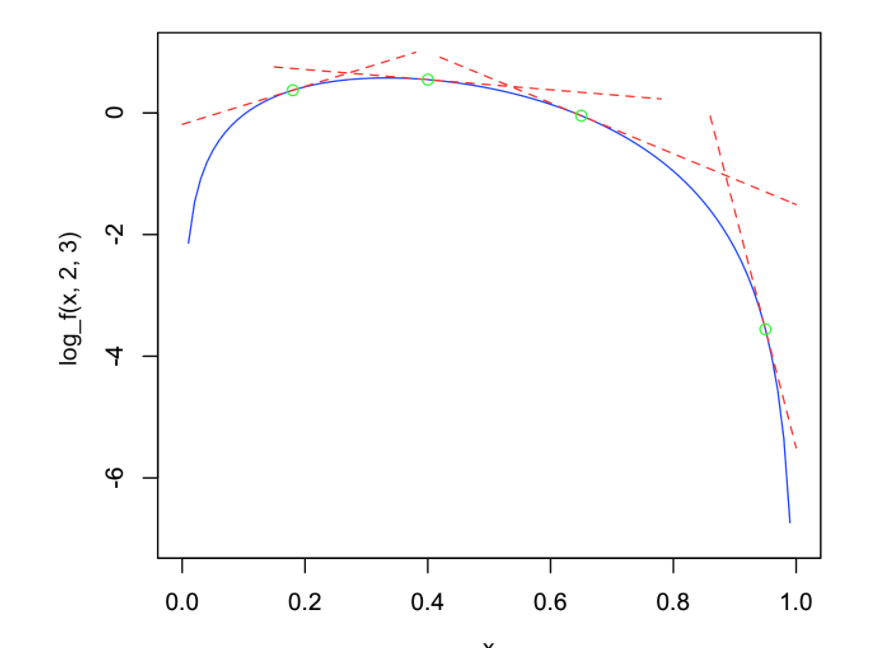
• 切平面转化为分段函数，分段函数紧紧包裹$f(x)$；
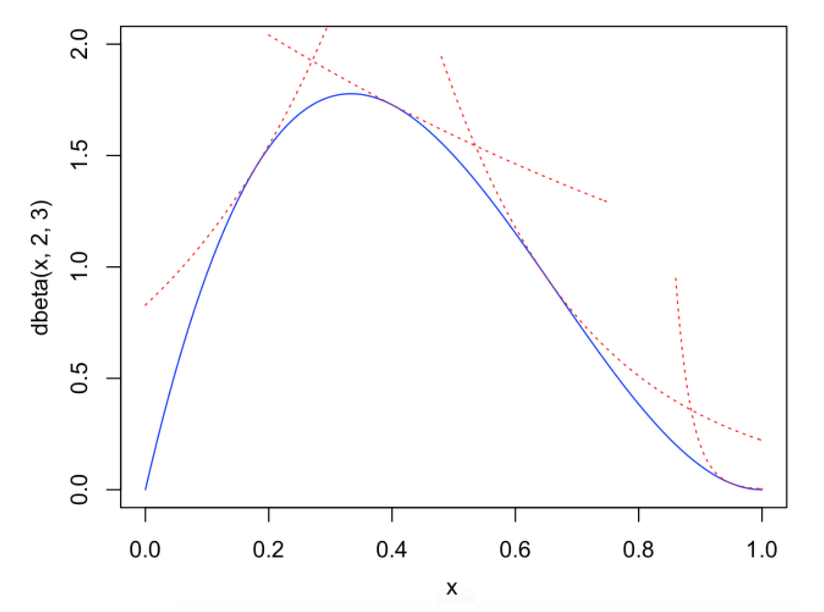
• 使用分段函数做为$f'(x)$进行reject sampling；

• ← Previous Post
• Next Post →