概述
假设我们想计算$E[f(x)]$,而$x$本身服从分布,即 如果我们不方便在上采样或者,可以引入一个方便采样的, 这样问题就转化成了求在分布下的期望。 $w(x)$称为importance weight, $q(x)$称为proposed distribution.
下图表示了$p(x)$很复杂,无法进行采样的情况。
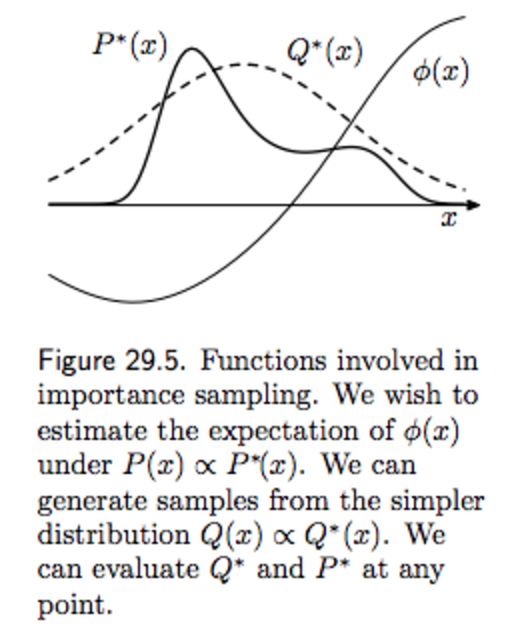
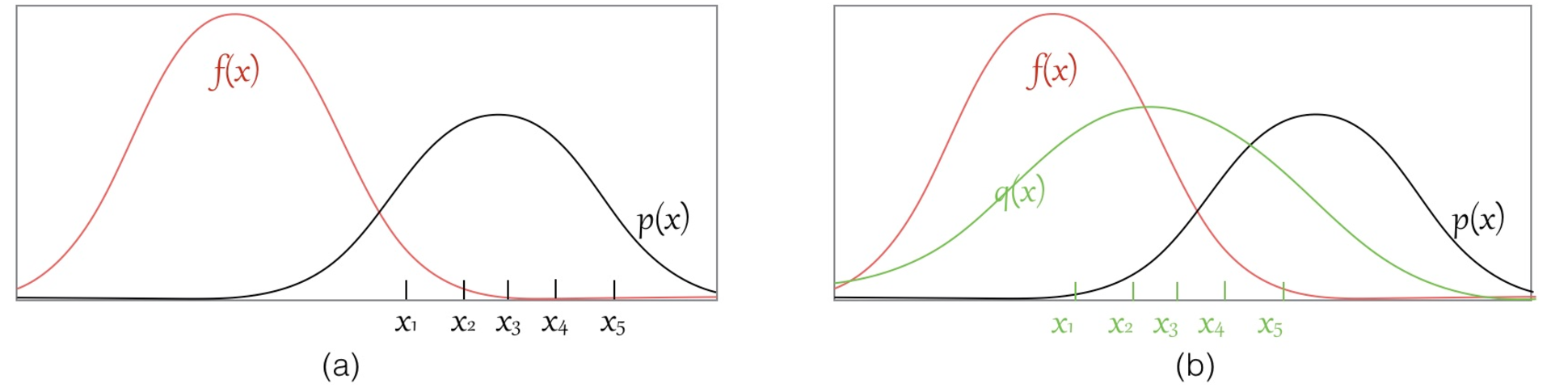
另外一种情况如下图所示,左图表示直接从$p(x)$进行采样,会导致$f(x)$大的地方都没有采样点,计算出来的期望可能有所偏差。右图中我们引入$q(x)$来协助采样,如果能在$f(x)p(x)$较大的地方获取较多的样本,则所获得的期望估计结果就能较准确地接近真实值。
一个实际的例子
一个工厂里面,工资有三档,低,中,高,分别为100块,200块,300块。其中拿低档工资的工人占60%,拿中档工资的工人占30%,拿高档工资的工人10%人。求该工厂工人工资的期望值。
这很容易,使用Monte Carlo Method即可。随机地对该厂工人采样,求均值,结果随着采样数量增加会收敛该式0.6N∗100+0.3N∗200+0.1N∗300N/N。
接下来,问题改变了。该工厂有一个车间,工人的收入分布有所不同。低档50%,中档30%,高档20%。假设我们只能从该车间工人中采样,如何得到该厂的工人工资的期望值。
如果我们直接从该车间工人中采样取均值,结果是错误的,因为车间工人工资分布与工厂工人工资分布是不同的,从车间工人中采样的结果应该收敛到该式0.5N∗100+0.3N∗200+0.2N∗300N/N,显然与上式不同。
因此,我们在用来自车间的工人采样时,只需要在工人工资数额前乘上一个权重p(x)/q(x),如对于低档次工资的工人,权重为0.6/0.5,中档0.3/0.3,高档0.1/0.2,把所采工人的工资按权重求均值,就是工厂工人工资的期望值。
Adaptive Importance Sampling & Sampling-Importance-Resampling
Parallel Adaptive Importance Sampling
Adaptive Importance Sampling via Stochastic Convex Programming
在高维空间里找到一个合适的 q(x) 非常难。即使有 Adaptive importance sampling 和 Sampling-Importance-Resampling(SIR) 的出现,find a proposal distribution q(x) which is both easy to sample and can produce good approximations, it is often impossible.