Reversible Markov Chain
According to wiki Markov Chain
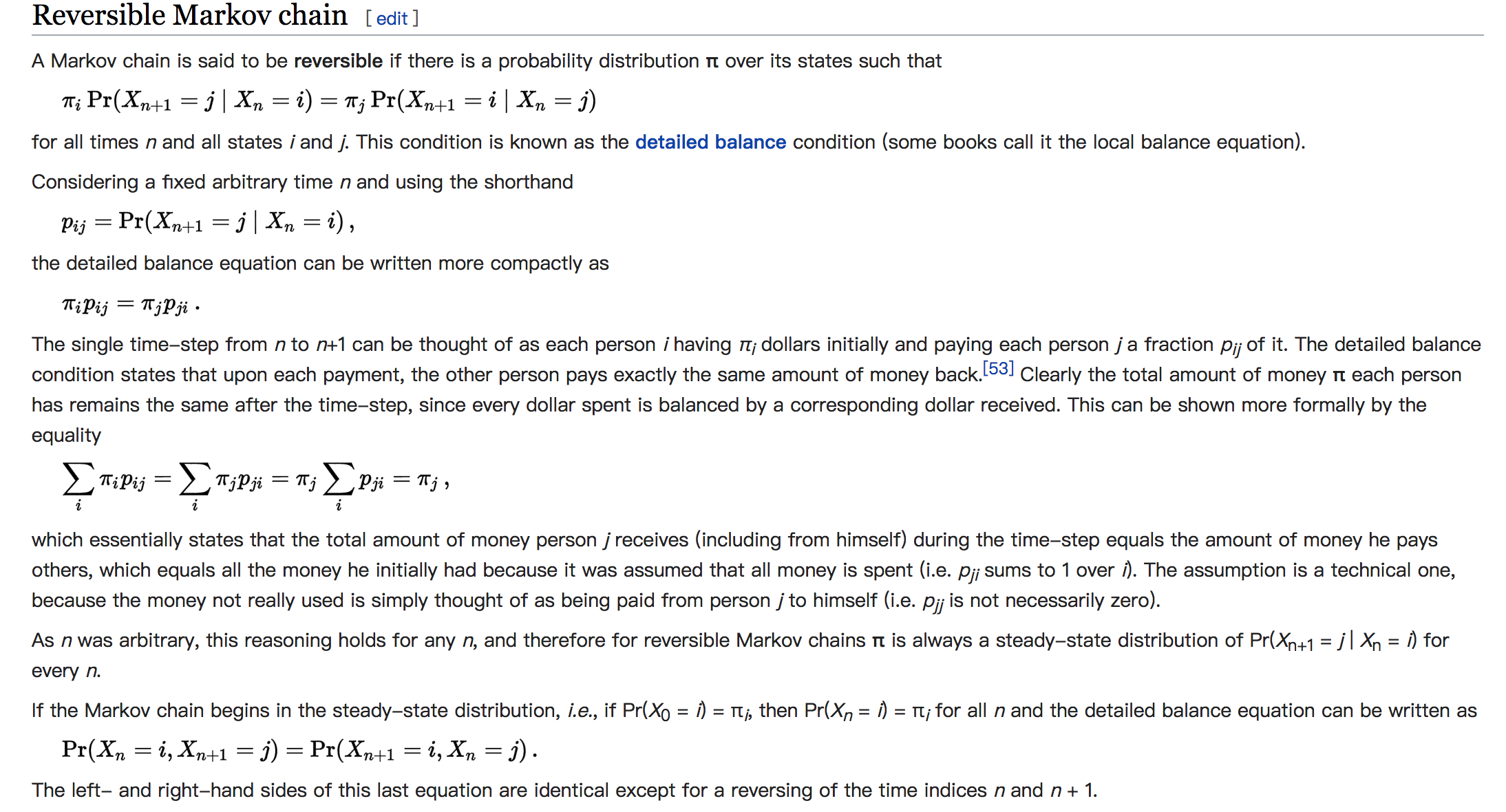

也就是说,符合detailed balance(细致平稳)条件的马尔科夫链是Reversible Markov Chain(可反转马尔科夫链)。
从n到n+1状态的过程可以看做:一个人$i$,初始手里有$π_i$个硬币 ,下一轮把其中$p_{ij}$比例的硬币给其它人$j$。detailed balance条件表明其他人$j$也会把同样数量的钱再返回给$i$。所以,最终每个人拥有硬币数量保持不变。$\pi$称为该马尔科夫链的平稳分布。
既然Reversible Markov可以趋近于平稳分布,那么我们可以构造一个平稳分布是$\pi$的马尔科夫链,来对目标分布$\pi$进行采样。我们从任何一个初始状态$x_0$出发沿着马尔科夫链转移, 得到一个转移序列 x0, x1, x2, ⋯xn, xn+1 ⋯,, 如果马尔科夫链在第n步已经收敛了,于是我们就得到了服从$\pi$分布的样本xn, xn+1⋯。
MCMC
Markov Chain Monte Carlo Method
In statistics, Markov chain Monte Carlo (MCMC) methods are a class of algorithms for sampling from a probability distribution based on constructing a Markov chain that has the desired distribution as its equilibrium distribution.
马尔科夫链蒙特卡洛方法,这这样一类算法的统称:通过构造一个平稳分布是目标采样分布的马尔科夫链,来进行采样的算法。
和Inverse Transforming Sampling、Reject Sampling、Importance Sampling不同,基于MCMC的采样,第i+1次的采样是依赖于第i次的采样的。
Metropolis-Hasting Algorithm
具体解释参考这里
采样目标分布为$p(x)$,proposal distribution的转移矩阵为$Q$,$q(i,j)$表示i到j的转移概率。 通常情况下,$p(i)q(i,j)\not=p(j)q(j,i)$,不满足detailed balance 我们增加一个参数,$p(i)q(i,j)\alpha(i,j)=p(j)q(j,i)\alpha(j,i)$ 其中,$\alpha(i,j)=p(j)q(j,i)$ $\alpha$可以看作是i跳转到j的时候接受概率 $q(i,j)p(j)q(j,i)$对应的$Q’可以看做是一个符合detailed balance条件的新的转移矩阵
基本的MCMC采样算法如下:

但是,接受概率偏小的时候,马尔科夫链可能会原地踏步,导致采样质量和效率低下。于是,我们对等式做一下改动,
取作为接受概率。就获得了Metropolis-Hasting算法。

Metropolis-Hasting示例
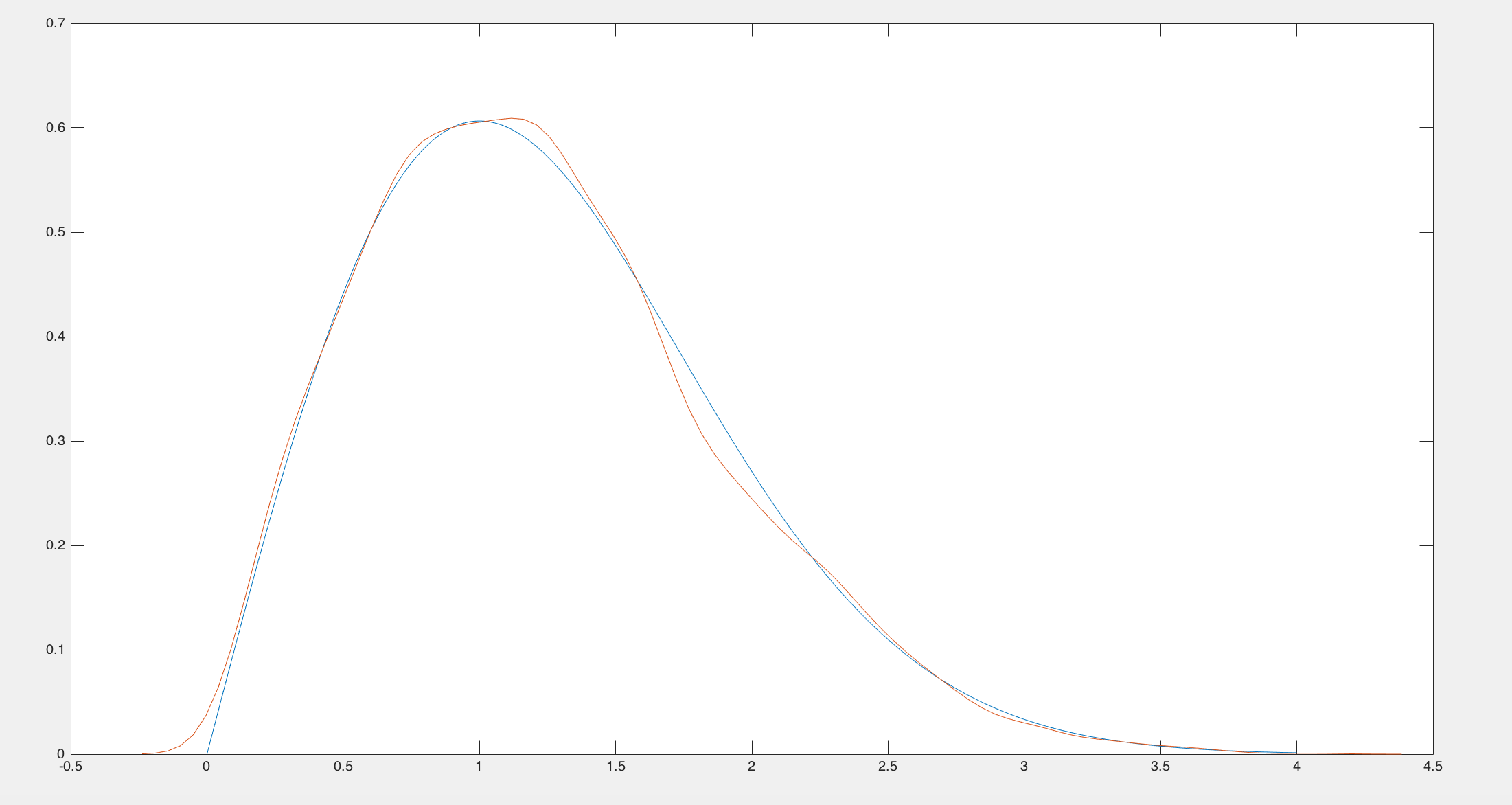
使用Chi-squared distribution做为proposal distribution来对Rayleigh distribution进行采样。
- Metropolis.m
round = 10000; x=(chi2rnd(1)); u=unifrnd(0,1,1,round); sigma = 1; acceptCount=0; for i=1:round xt=x(i); y=chi2rnd(xt); acceptRate=raylpdf(y,sigma)*chi2pdf(xt,y)/(raylpdf(xt,sigma)*chi2pdf(y,xt)); if u(i) < min(acceptRate,1) x=[x,y]; else x=[x,xt]; acceptCount=acceptCount+1; end end % plot rayleigh distribution pdf xPlot=(0:0.01:4); yPlot=raylpdf(xPlot,sigma); plot(xPlot,yPlot); hold on; ksdensity(x(1000:round));
Gibbs Sampling
Gibbs Sampling可以认为是Metropolis-Hasting算法的一种特例。对于高维的采样,由于accept-rate的存在,采样效率会更为低下。
先看下二维的情况,假设有概率分布p(x,y),有x坐标相同的两个点$A(x_1,y_1)$和$B(x_1,y_2)$,有: 所以 即
上式表明了,对于在这条直线上的转移,如果转移概率为 ,则符合detailed balance。
同样的,对于y=y1的直线上两点A和B,有:
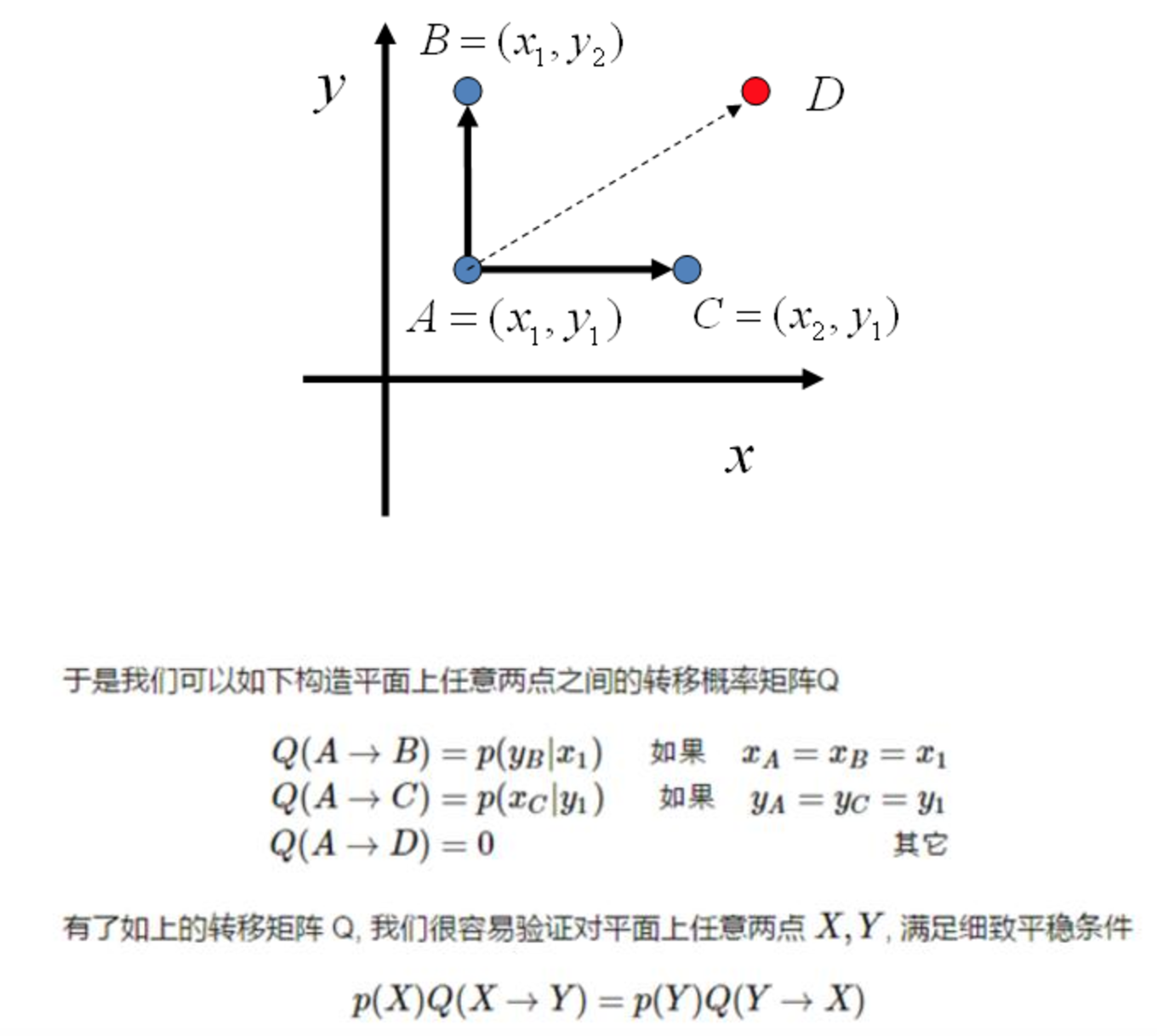
于是这个二维空间上的马尔科夫链会收敛到平稳分布p(x,y)。于是得到了二维空间上的Gibbs Sampling算法。

注意点:
- 在t时刻,随机选择x轴或者y轴进行条件转移,无需每次都进行坐标轴轮换
- 目标分布满足
扩展到多维的情况:
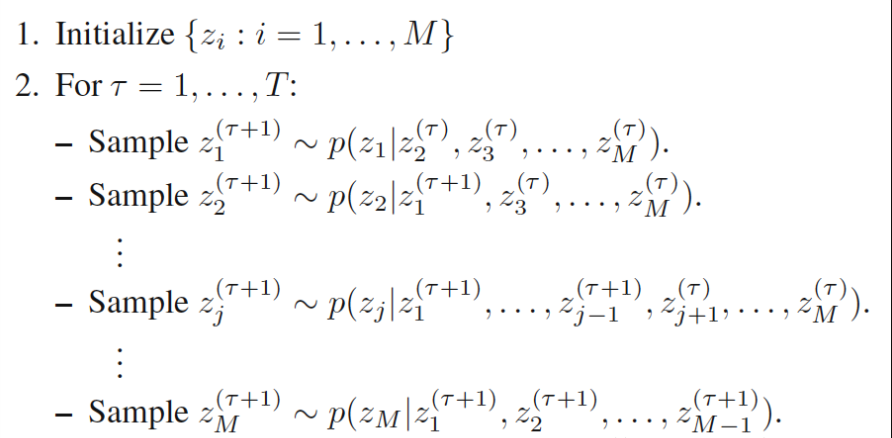
以上算法收敛后,得到的就是概率分布p(x1,x2,⋯,xn)的样本。